Introduction to Semi-Supervised Learning with Ladder Networks
Today, deep learning is mostly about pure supervised learning. A major drawback of supervised learning is that it requires a lot of labeled data and It is quite expensive to collect them. So, deep learning in the future is expected to unsupervised, more human-like.
“We expect unsupervised learning to become far more important in the longer term. Human and animal learning is largely unsupervised: we discover the structure of the world by observing it, not by being told the name of every object.”
– LeCun, Bengio, Hinton, Nature 2015
Semi-Supervised Learning
Semi-supervised learning is a class of supervised learning tasks and techniques that also make use of unlabeled data for training - typically a small amount of labeled data with a large amount of unlabeled data.
So, how can unlabeled data help in classification? Consider the following example (taken from these slides) consisting of only two data points with labels.
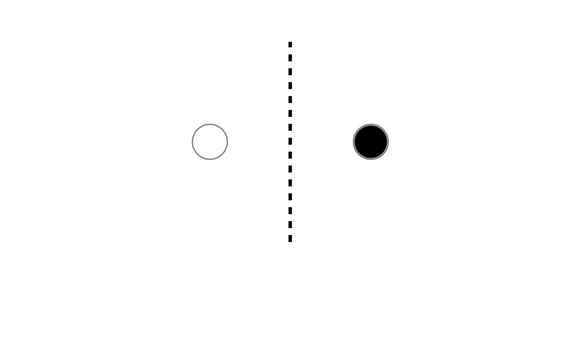
How would you label this point?
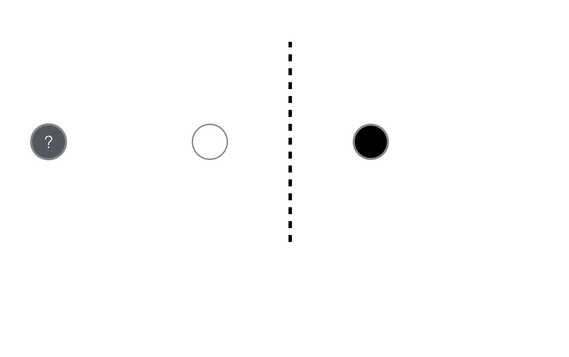
What if you see all the unlabeled data?
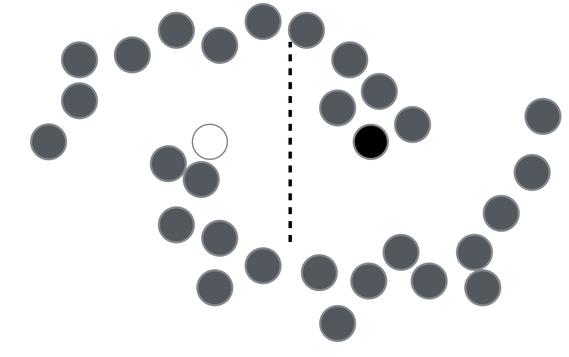
In order to make any use of unlabeled data, we must assume some structure to the underlying distribution of data. Labels are homogeneous in densely populated space ie., data points close to each other belong to the same class (smoothness assumption). Iterating this assumption over the data points until all data points are assigned a label,
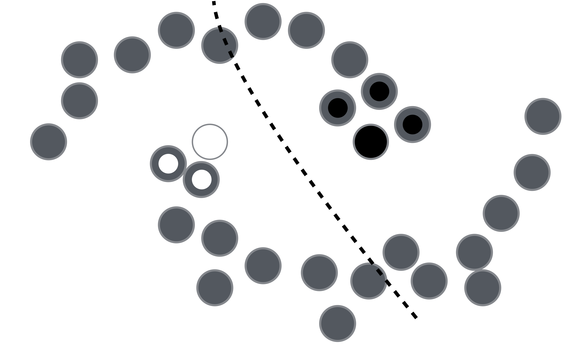
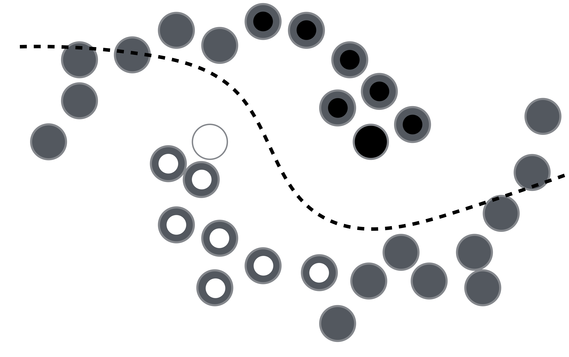
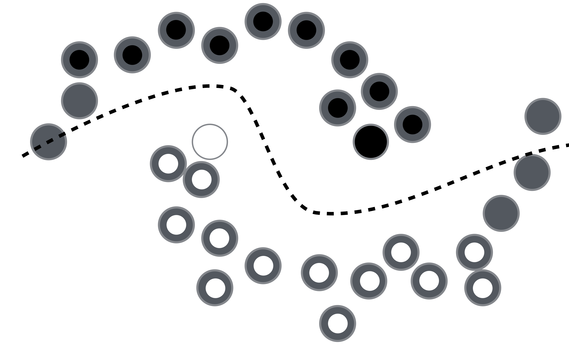
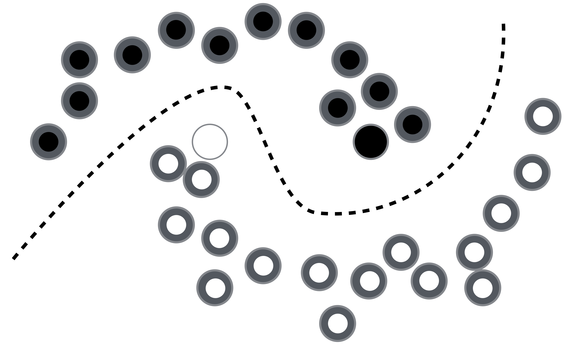
It has been discovered that the use of unlabeled data together with a small amount of labeled data can improve accuracy considerably. The collection of unlabeled data is inexpensive relative to labeled data. Often labeled data is scarce and unlabeled data is plentiful. In such situations, semi-supervised learning can be used. Also, much of human learning involves a small amount of direct instruction (labeled data) combined with large amounts of observation (unlabeled data). Hence, semi-supervised learning is a plausible model for human learning.
Ladder Networks
Ladder networks combine supervised learning with unsupervised learning in deep neural networks. Often, unsupervised learning was used only for pre-training the network, followed by normal supervised learning. In case of ladder networks, it is trained to simultaneously minimize the sum of supervised and unsupervised cost functions by backpropagation, avoiding the need for layer-wise pre-training. Ladder network is able to achieve state-of-the-art performance in semi-supervised MNIST and CIFAR-10 classification, in addition to permutation-invariant MNIST classification with all labels.
Key Aspects
Compatibility with supervised methods
It can be added to existing feedforward neural networks. The unsupervised part focuses on relevant details found by supervised learning. It can also be extended to be added to recurrent neural networks.
Scalability resulting from local learning
In addition to a supervised learning target on the top layer, the model has local unsupervised learning targets on every layer, making it suitable for very deep neural networks.
Computational efficiency
Adding a decoder (part of the ladder network) approximately triples the computation during training but not necessarily the training time since the same result can be achieved faster through the better utilization of the available information.
Implementation
This is a brief introduction to the implementation of Ladder networks. A detailed and in-depth explanation of Ladder network can be found in the paper “Semi-Supervised Learning with Ladder Networks”.
The steps involved in implementing the Ladder network are typically as follows:
- Take a feedforward model which serves supervised learning as the encoder. The network consists of 2 encoder paths - clean and corrupted encoder. The only difference is that the corrupted encoder adds Gaussian noise at all layers.
- Add a decoder which can invert the mappings on each layer of the encoder and supports unsupervised learning. Decoder uses a denoising function to reconstruct the activations of each layer given the corrupted version. The target at each layer is the clean version of the activation and the difference between the reconstruction and the clean version serves as the denoising cost of that layer.
- The supervised cost is calculated from the output of the corrupted encoder and the output target. The unsupervised cost is the sum of denoising cost of all layers scaled by a hyperparameter that denotes the significance of each layer. The final cost is the sum of supervised and unsupervised cost.
- Train the whole network in a fully-labeled or semi-supervised setting using standard optimization techniques (such as stochastic gradient descent) to minimize the cost.
An illustration of a 2 layer ladder network,
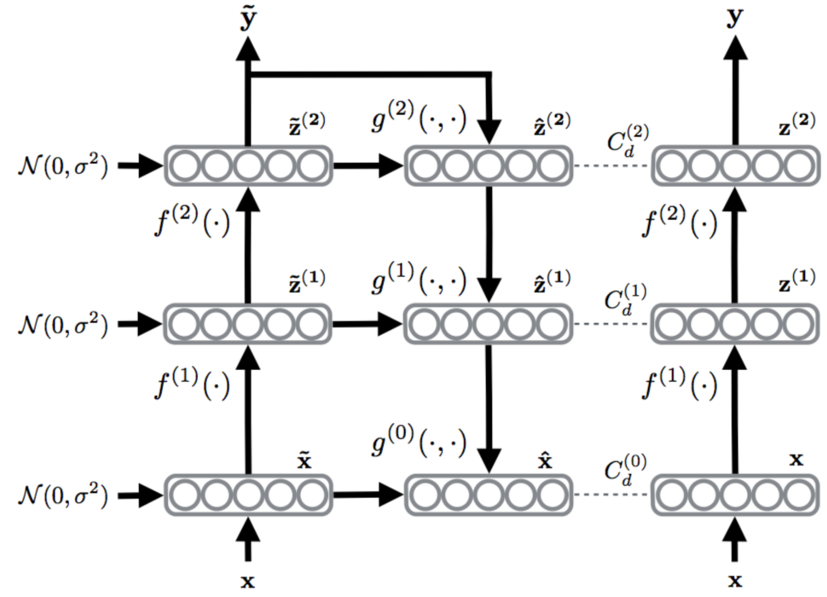
Batch normalization is applied to each preactivation including the topmost layer to improve convergence (due to reduced covariate shift) and to prevent the denoising cost from encouraging the trivial solution (encoder outputs constant values as these are the easiest to denoise). Direct connection between a layer and it’s decoded reconstruction are used. The network is called a Ladder network because the resulting encoder/decoder architecture resembles a ladder.

Conclusion
The performance of Ladder networks is very impressive. On MNIST, it achieves an error rate of 1.06% with only 100 labeled examples! This is much better than previous published results, which shows that the method is capable of making good use of unsupervised learning. However, the same model also achieves state-of-the-art results and a significant improvement over the base-line model with full labels in permutation invariant MNIST classification, which suggests that the unsupervised task does not disturb supervised learning.
Ladder network is simple and easy to implement with many existing feedforward architectures, as the training is based on backpropagation from a simple cost function. It is quick to train and the convergence is fast, thanks to batch normalization.
Code
The code published along with the original paper is available here - https://github.com/CuriousAI/ladder. My implementation of Ladder networks in TensorFlow is available here - https://github.com/rinuboney/ladder. Note: The TensorFlow implementation achieves an error rate about 0.2% - 0.3% more than the error rates published in the paper.
Related papers
Semi-supervised learning using Ladder networks was introduced in this paper:
Ladder network was further analyzed and some improvements that attained an even better performance were suggested in this paper:
and finally, these are the papers that led to the development of Ladder networks:
- Rasmus, Antti, Tapani Raiko, and Harri Valpola. “Denoising autoencoder with modulated lateral connections learns invariant representations of natural images.” arXiv preprint arXiv:1412.7210 (2014).
- Rasmus, Antti, Harri Valpola, and Tapani Raiko. “Lateral Connections in Denoising Autoencoders Support Supervised Learning.” arXiv preprint arXiv:1504.08215 (2015).
- Valpola, Harri. “From neural PCA to deep unsupervised learning.” arXiv preprint arXiv:1411.7783 (2014).